Research

LeanHammer: A Domain-General Hammer for Lean

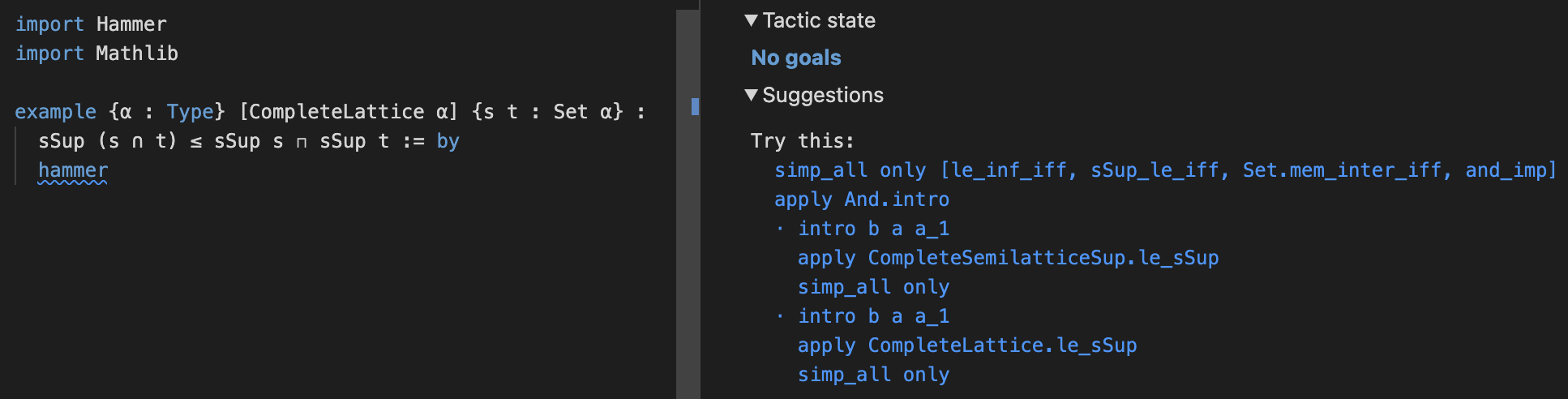
In an interactive theorem proving context, a hammer is a tool that integrates premise selection, translation to external automatic theorem provers, and proof reconstruction into one overarching tool to automate tedious reasoning steps. In Isabelle/HOL, the general purpose automation provided by Sledgehammer has become an essential part of the typical user's workflow.

Much of my research has related to the development of a hammer for Lean. Thomas Zhu, Sean Welleck, Jeremy Avigad, and I developed LeanPremise, a neural premise selector specifically trained for a Lean Hammer. I have contributed to Lean-auto, an interface between Lean and automated theorem provers developed primarily by Yicheng Qian. I also developed Duper, a superposition theorem prover for dependent type theory, along with Yicheng Qian, Jeremy Avigad, and Alexander Bentkamp. Each of these projects serve as components in LeanHammer, an end-to-end domain general hammer for Lean.

Hint-Based SMT Proof Reconstruction

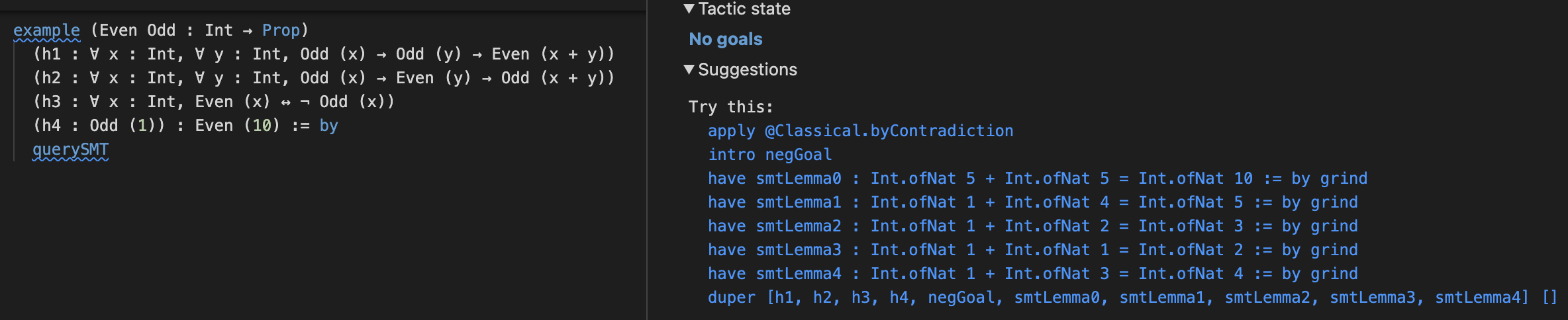
There are several paradigms for integrating interactive and automated theorem provers, combining the convenience of powerful automation with strong soundness guarantees. These paradigms vary both in how they translate problems between the technologies' respective languages, and in how they leverage proofs discovered by automation.

My research with Haniel Barbosa and Jeremy Avigad explores a new approach to reconstructing proofs found by SMT solvers. Rather than verifying or replaying a full proof produced by the SMT solver, or at the other extreme, rediscovering the solver’s proof from just the set of premises it uses, we explore an approach which helps guide an interactive theorem prover’s internal automation by leveraging derived facts during solving. This enables our Lean tactic, QuerySMT, to use hints disocvered by cvc5 to generate structured proof scripts which don't depend on the external solver.

Duper: An Automatic Theorem Prover for Dependent Type Theory

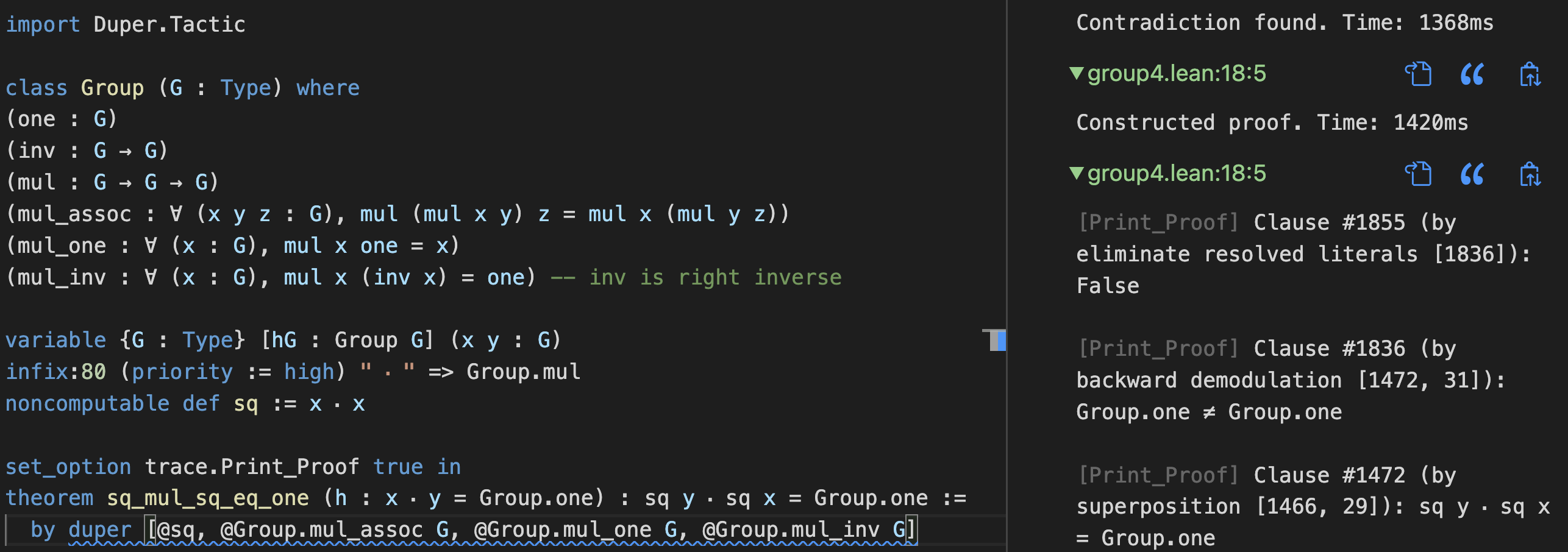
One of the most important factors impacting the usability of an interactive theorem prover (ITP) is the power of its automation. For example, in Isabelle/HOL, the general purpose automation provided by Metis and Sledgehammer has become an essential part of the typical user's workflow.

Most current ITP automation is either targeted to a particular domain or designed primarily for first-order logic. But most ITPs support languages much richer than that of first-order logic. My research with Yicheng Qian, Jeremy Avigad, and Alexander Bentkamp concerns general-purpose ITP automation designed to effectively operate in Lean's dependently typed setting. Together we are developing Duper, an automatic theorem prover in Lean 4 based on the superposition calculus. To learn more about Duper, feel free to read this conference paper.

A Formalized Reduction of Keller's Conjecture

If you attempted to entirely cover a 2-dimensional Euclidean plane with non-overlapping unit squares, you would quickly find that it is necessary to have at least two squares share a complete edge. Similarly, if you attempted to fill a 3-dimensional Euclidean space with non-overlapping unit cubes, you would find that it is necessary to have at least two cubes share a complete face.

Keller's Conjecture states that this trend holds in arbitrary dimensions. As it turns out, Keller's Conjecture is true in 7 or fewer dimensions, and is false in 8 or more dimensions.

The proof that Keller's Conjecture holds in 7 dimensions critically relies on a reduction from the original geometric conjecture to a finite graph clique problem. My research involved using the Lean 3 theorem prover to formalize and verify this reduction. I also used this formalized reduction to produce the first verified proof that Keller's Conjecture is false in 8 dimensions. You can read more about this work here, and you can check out the formal proofs here.

A Polymorphic Logical Framework

The LF logical framework is a formal system designed to provide a general means of presenting deductive systems. But the ease with which a logical framework can present certain deductive systems and support various applications depends significantly on the language features provided by that framework. For this reason, attention has been given to areas in which LF can be improved for certain applications, yielding extensions to LF such as LLF (a linear logical framework), RLF (a logical framework for relevant logics), and CLF (a concurrent logical framework).

My research with Karl Crary involved developing an extension to LF that supports representing and reasoning about polymorphic types. The primary aims for this work were to define the extension’s type system and semantics, validate it by proving that the system honors identity expansion and cut admissibility, and potentially formalize the extension and the proofs that validate it in Coq.

Program Equivalence for Assisted Grading of Functional Programs

In courses that involve programming assignments, giving meaningful feedback to students is an important challenge. In a perfect world, every student would receive personalized human feedback. But as computer science courses grow in demand, this ideal is increasingly costly.

To make human feedback more accessible, even as class sizes grow considerably, I worked with Vijay Ramamurthy, Ruben Martins, and Umut Acar to create Zeus. Zeus is a tool that can take a set of programs written in Standard ML, and, using the SMT solver Z3, partition them into buckets of provably equivalent programs. This makes it possible to simultaneously give human feedback to all students that implemented the same algorithm or made the same error.

To learn more about how Zeus is designed, and how it can be used to make human feedback more accessible, feel free to watch my OOPSLA talk embedded above. For more information on Zeus' theoretical foundations, you can read our conference paper here and its extended version here.